what is false positive

Contingency table. True Positive, False Positive, False Negative ...

In, and more common, false positive is an error in which the results of the tests are not correctly indicate the conditions, such as disease (positive results), when in fact it is not present, while a false negative is an error in which the test results are not true showed no presence of the condition (negative result), when in fact it is present. These are the two types of errors in (and contrasted with the correct result, both true positive or negative is true.) They are also known in medicine as a false positive diagnosis (respectively negative), and as a false positive (respectively negative) error , A false positive is different from overdiagnosis, and also different from overtesting.

In the analogous concept known as, where positive results corresponded to resist, and negative results do not conform to reject the null hypothesis. The term is often used interchangeably, but there are differences in detail and interpretation because of the differences between medical and statistical hypothesis testing.

A false positive error, or false positive brevity, commonly called a "false alarm", is a result that indicates a certain condition exists, when it is not. For example, in the case of "", the condition is tested for the "No wolf near the herd" ?; one shepherd initially indicated there was one, by calling "Wolf, wolf!"

A false positive error is where the test is checking a single condition, and one gives (positive) affirmative decision. However it is important to distinguish between type 1 error rate and the probability of being a false positive result. The latter is known as a false positive risks (see).

A false negative error, or false negatives in short, is a test showing that the condition does not hold, it is not. In other words, wrong, no effect has been concluded. Examples of false negatives is a test shows that a woman is not pregnant while she was actually pregnant. Another example is truly innocent prisoners are freed from evil. the condition of "innocent prisoners" holding (the prisoner was guilty). But the test (a test in a court of law) fail to be aware of this condition, and one decides that prisoners are not guilty, concluding false negative about the condition.

A false negative error is occurred in a test in which a single condition is checked for and the results of the test is wrong that these conditions are not present.

is the proportion of all the negatives that still gives a positive test result, that is, the conditional probability of a positive test result given an event that is not present.

equal to the rate of false positives. The of the test is equal to 1 minus the false positive rate.

In, this fraction is given the Greek letter α and 1-α is defined as the specificity of the test. Increase the specificity test lowers the chances of a type I error, but raises the possibility of a type II error (false negatives that reject the alternative hypothesis when it is true).

complementary, false negative rate is the proportion of positive produce negative test results to the test, that is, the conditional probability of a negative test result given that conditions were looking for a present.

In, this fraction is given the letter β. The "" (or "") of the test is equal to 1-β.

The term false discovery rate (FDR) was used by Colquhoun (2014) means the probability that a "significant" result is a false positive. Then Colquhoun (2017) uses the term risk of false positives (FPR) for the same amount, to avoid confusion with the term FDR as used by people who are working on some comparisons. Correction for multiple comparisons only intended to correct a type I error rate, so the result is (corrected) p value. Leaving them vulnerable to misinterpretation as other p value. The risk of false positives always higher, often much higher, than the p-value. These two ideas confusion, mistake of diverted conditional, has caused a lot of damage. Because of the ambiguity of notation in this field, is essential to look at the definition of each paper. The dangers of dependence on the p-value is emphasized in Colquhoun (2017) by showing that even a sighting of p = 0.001 is not necessarily strong evidence against the null hypothesis. Despite the fact that the odds ratio supports the alternative hypothesis on zeros close to 100, if the hypothesis was not unreasonable, the prior probability of the real effect to 0.1, p = 0.001 observation even going to have a false positive rate the of 8 percent. It will not even reach the level of 5 percent. As a result, it has been recommended that each value of p must be accompanied by a prior probability of there being a real effect that would be required to assume to achieve the risk of false positives from 5%. For example, if we observe the p = 0.05 in a single experiment, we will have 87% sure that there is a real effect before the experiments were carried out to achieve the risk of false positives from 5%.

The article "" discuss the parameters in statistical signal processing based on the ratio of errors of various types.

In many legal traditions exist, as stated in:

That is, the false negatives (the guilty freed and go without punishment) is far more detrimental than false positives (innocent people are punished and suffered). This is not universal, however, and some systems prefer to prison many innocent, rather than allowing the guilty to escape single -. Tradeoff vary between legal traditions []

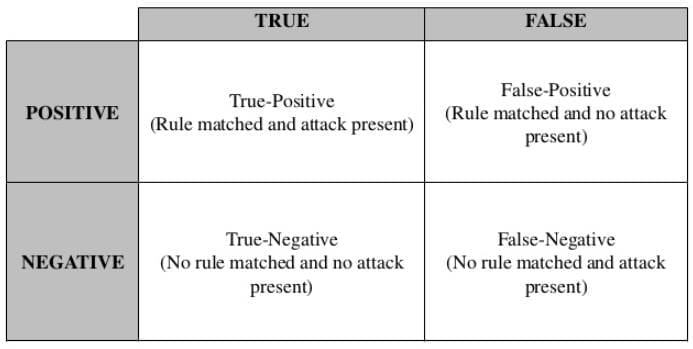False positive, false negative, true positive, and true negative ...
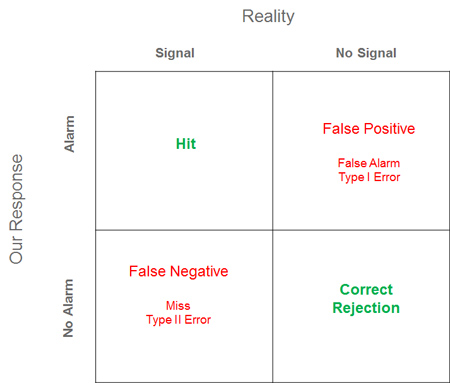MeasuringU: Managing False Positives in UX Research
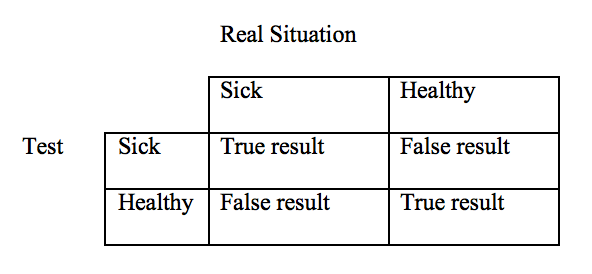False Positive vs. False Negative | AMS Grad Blog
Sources of eDNA false positive and false negative detections ...
Why Stats Engine controls for false discovery instead of false ...
What is the best example for false negative, false positive, true ...
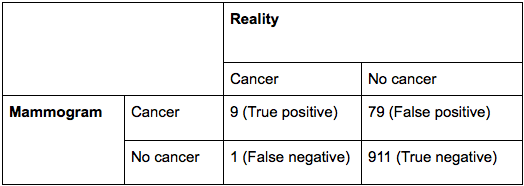False Positives and False Negatives - Explanation and examples ...
False False Positive Rates | NEJM
File:False-Positive-and-False Negative Psych-Evaluation ...
Definitions of true positive, false positive, false negative and ...
What is the opposite of a "false positive"? - English Language ...
The False-positive to False-negative Ratio in Epidemiologic ...
Machine Learning Accuracy: Learn the Metric to Assess ML Models ['20]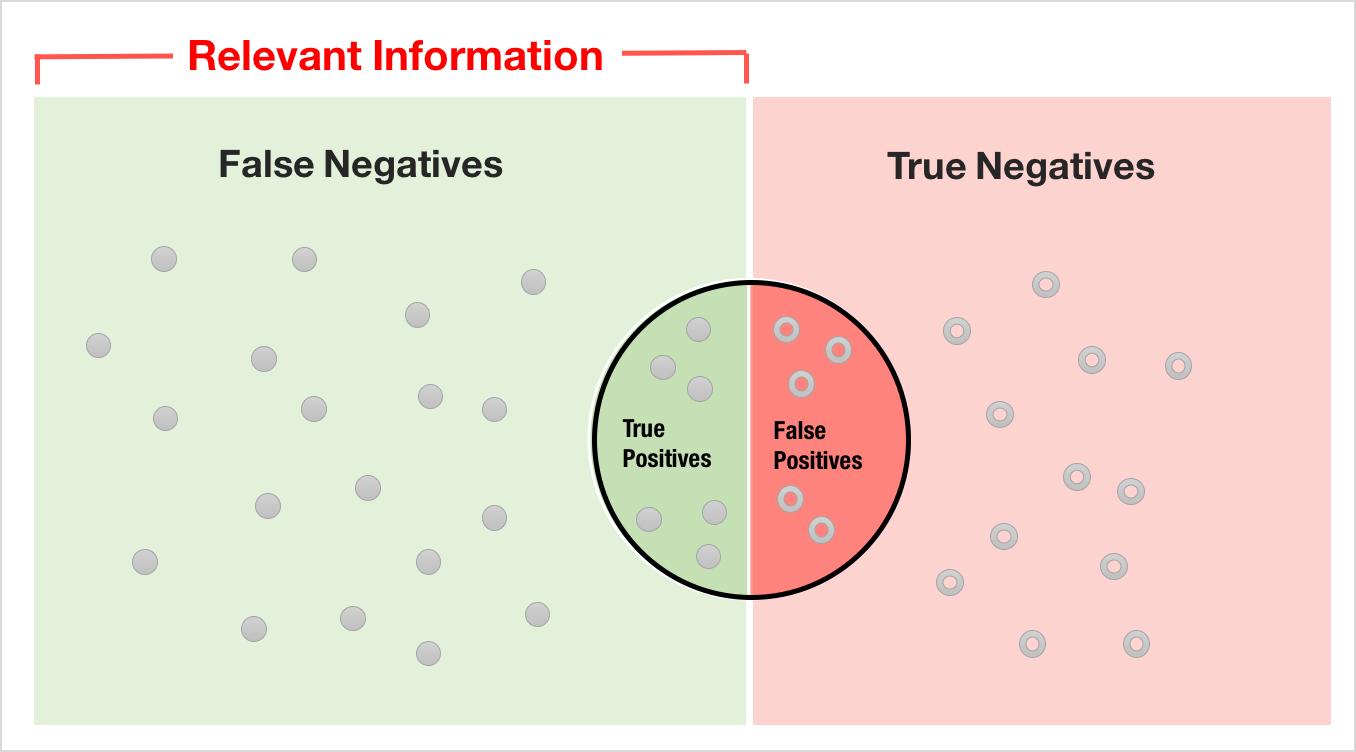
False Negatives: A Serious Danger in Your AML Program ...
Sensitivity and specificity - Wikipedia
FPR (false positive rate) vs FDR (false discovery rate) - Cross ...
AI Made to Reduce False Positives | Celent
Taking the Confusion Out of Confusion Matrices - Towards Data Science
False-Positive Psychology" by Simmons, Nelson, Simonsohn - YouTube
The micro-guide to spam terminology: false positives, false ...
Confusion matrix for model performance. False Positive rate/False ...
False Positives and the Base Rate Fallacy | Phoenix Area Skeptics ...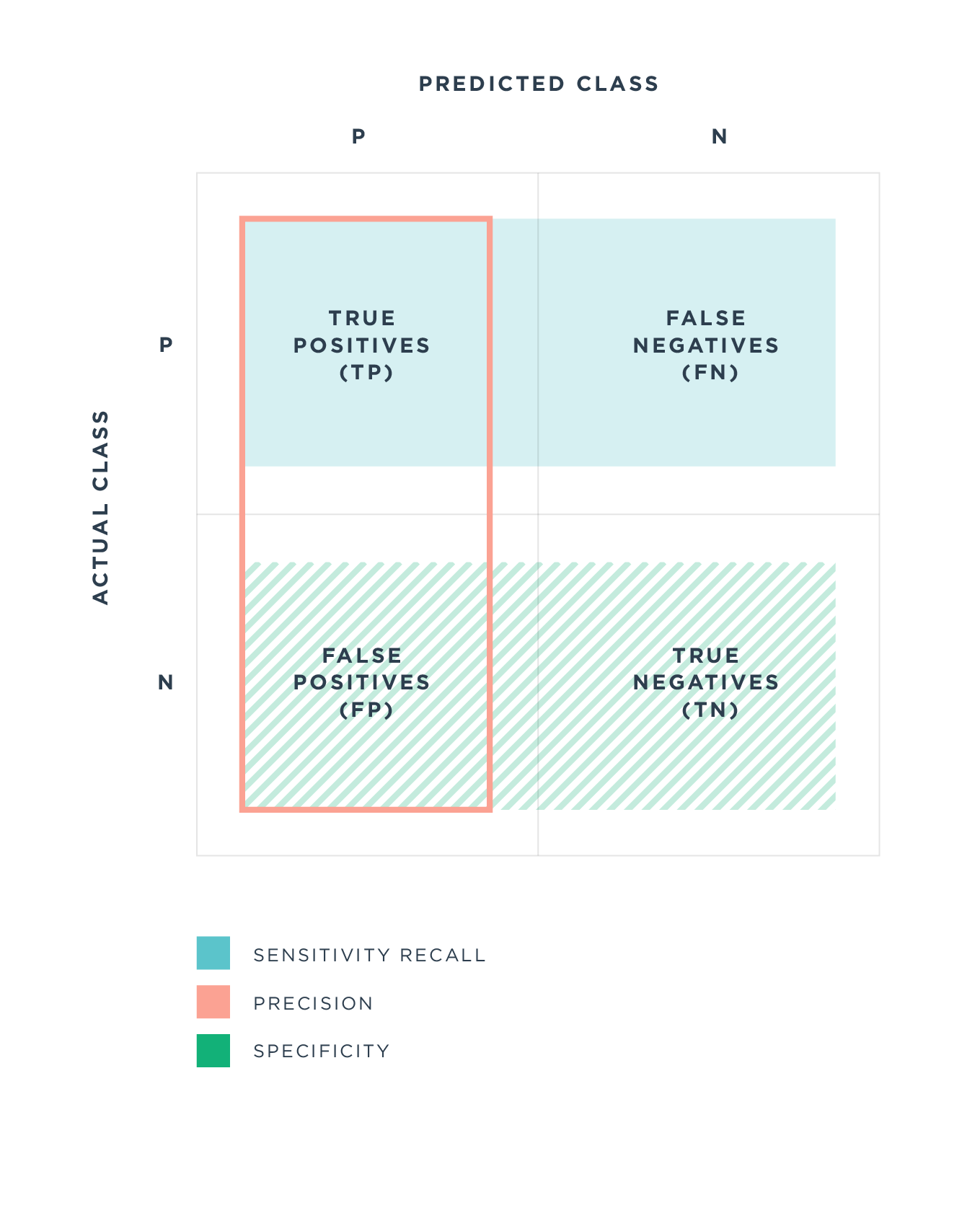
Fin - Adjustments, error types, and aggressiveness in fraud modeling
False Positives and Negatives: The Plague of Cybersecurity ...
False positive and false negative in software testing | Rapita Systems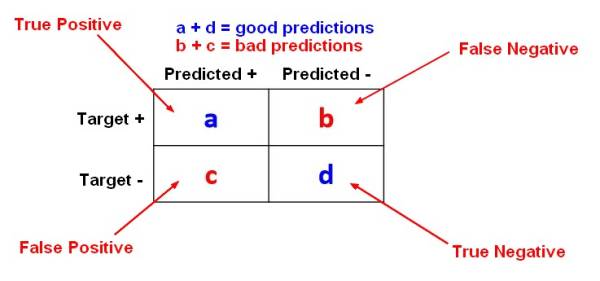
Statistics Learning - (Error|misclassification) Rate - false ...
What is the difference between false positive and false negative ...
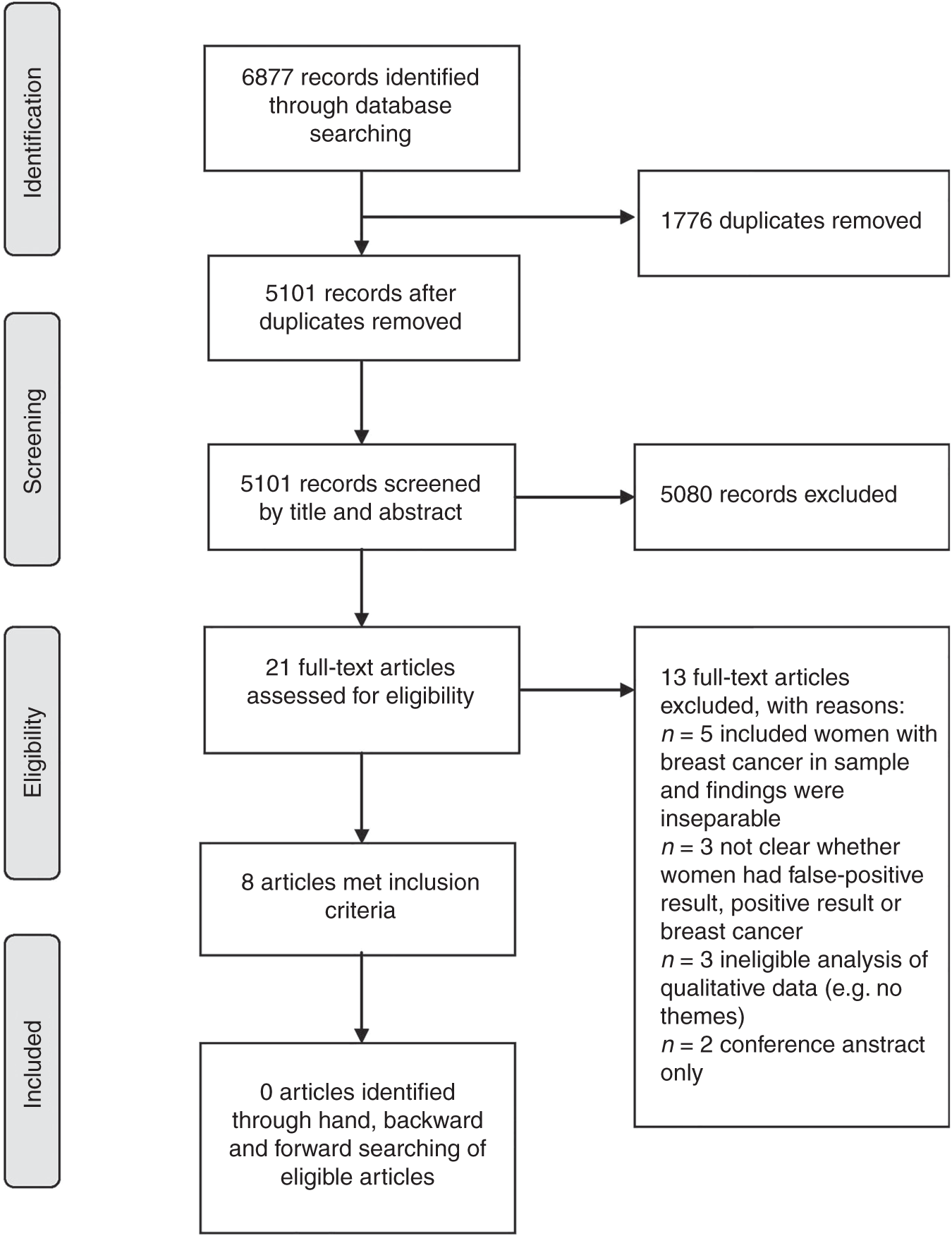How do women experience a false-positive test result from breast ...
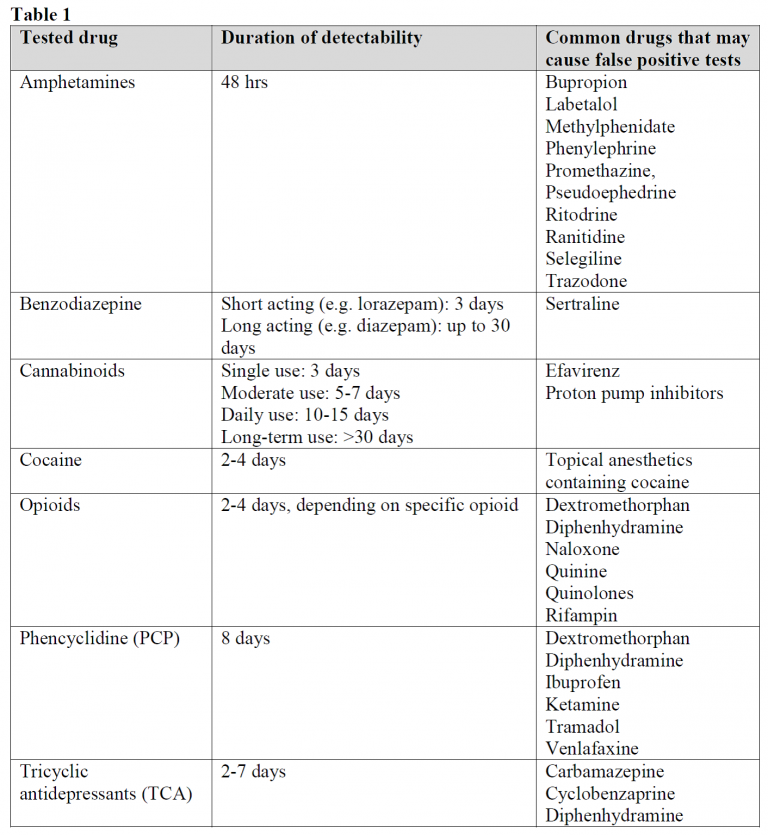Urine Drug Screens - Common drugs that may cause false positive tests
Solved: HW 9: False Positive And False Negative 1. Some "t ...
False positive, false negative, true positive, and true negative ...
False Positive False Negative Ex 1 - YouTube
Urine drug screens: When might a test result be false-positive ...
The Curious Case of False Positives in Application Security ...
What is False Positive? – Smartpedia – t2informatik
Findings on False Positive & False Negative in Testing - TestOrigen
Figure 1, Observed sensitivities and false-positive rates for the ...
False Negatives and False Positives – Playing Lean
Urine drug screens: When might a test result be false-positive ...
Cases in Urine Drug Monitoring Interpretation: How to Stay in Control
What is the best example for false negative, false positive, true ...
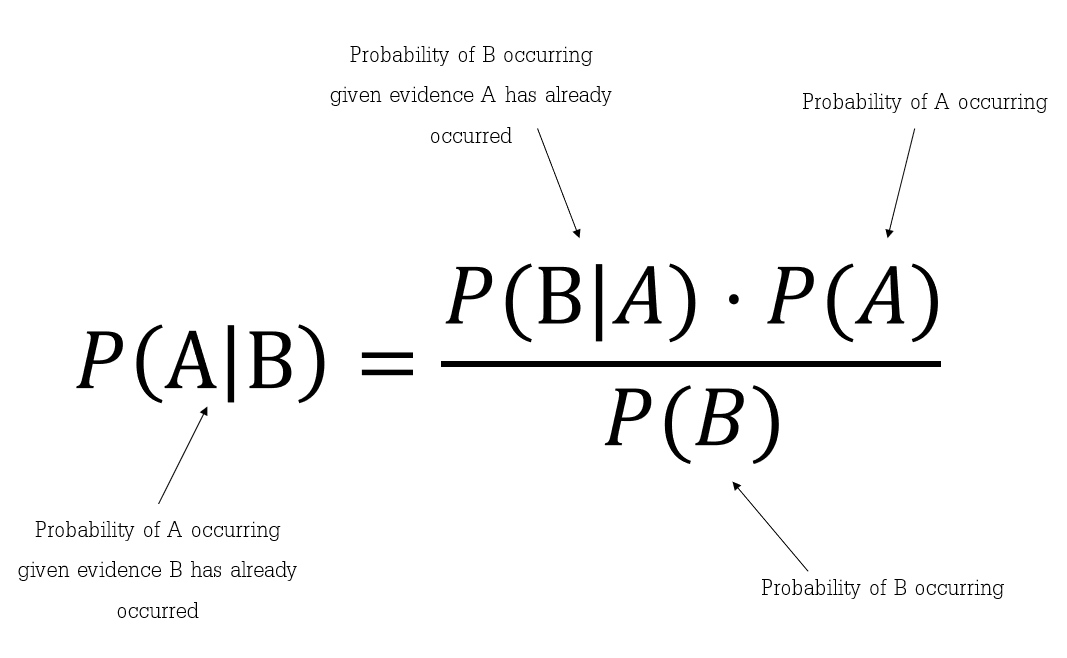How to Decipher False Positives (and Negatives) with Bayes ...
Recommended: False-Positive Psychology | PMean
Sensitivity and specificity - Wikipedia
How To Tell If a Virus Is Actually a False Positive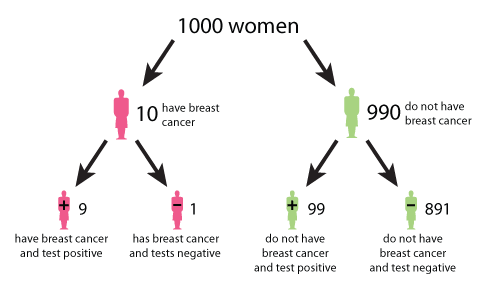
Maths in a minute: False positives | plus.maths.org
Solved: McAfee Support Community - False positive detection ...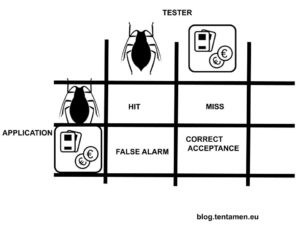
What Is False Positive Bug? – Tentamen Software Testing Blog
False Positives Sink Antivirus Ratings | PCMag
Ask The Expert April 2015: What can cause a false positive urine ...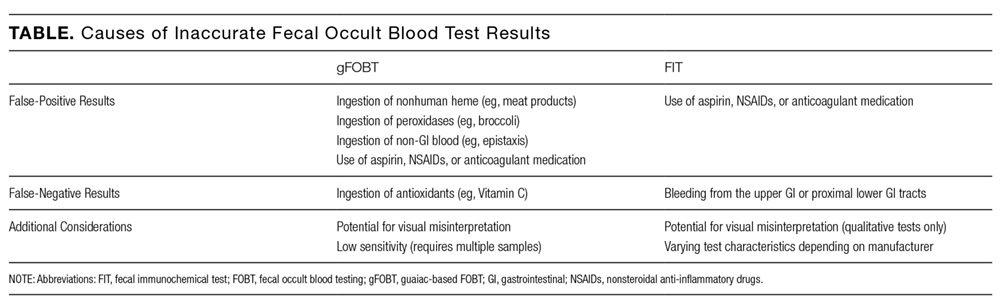
Causes of Inaccurate Fecal Occult Blood Test Results False ...
What are false positive and false negative in information security ...
What does it mean false positive in computing? And false negative?
Ten-Year Risk of False Positive Screening Mammograms and Clinical ...